Réussir une mise en page. — L’interlignage (4)

Distance entre deux lignes consécutives, l’interlignage est l’un des paramètres les plus importants de la maquette, s’agissant du texte courant, dont il conditionne en grande partie la lisibilité.

Pour déterminer une valeur satisfaisante, le billet précédent proposait une méthode de calcul intégrant à la fois force de corps, hauteur d’x et justification. Dans la mesure toutefois où elle ignore certains paramètres susceptibles d’influencer l’interlignage, impossibles à extraire directement des fontes et sans doute plus difficiles à mettre en équation, on se gardera bien d’y voir une formule clés en main qui donnerait dans tous les cas le meilleur résultat possible. Du reste, il existe encore des critères plus généraux, en fonction des intentions esthétiques du maquettiste.

Pour autant, quelle que soit la valeur qui aura été définie pour l’interlignage, une question reste en suspens qu’il faudra bien traiter dans tous les cas.

Dernière étape

Une fois défini notre interlignage théorique idéal, nous sommes face à un choix : conserver cette valeur, ou bien l’ajuster pour faire en sorte que la hauteur du rectangle d’empagement corresponde exactement au nombre entier de lignes qu’il est en mesure d’accueillir. Donne-t-on la priorité à l’interlignage ou bien à l’empagement ? Si l’écart entre hauteur des lignes et hauteur théorique du rectangle d’empagement est faible, moins de 2 pt, a-t-on vraiment besoin de rectifier l’interlignage ? Mais si cette différence est de plus de 5 pt, de 10 pt… ? En même temps, moins l’écart sera grand et plus l’impact de la rectification sur l’interlignage sera faible ; plus l’écart sera important, plus cet impact sera notable sur l’interlignage. Au maquettiste de trancher.

Voici en tout cas comment procéder à cet ajustement.

Calcul du nombre de lignes

En fonction de l’interlignage provisoire, il est possible de calculer le nombre de lignes de texte que peut accueillir le rectangle d’empagement d’une page pleine. On commence par déterminer la position de la première ligne par rapport au bord supérieur de la colonne de texte.

Première et dernière lignes d’une page pleine sont en effet tout aussi importantes l’une que l’autre dans la mesure où ce sont elles qui matérialisent le rectangle d’empagement aux yeux du lecteur. S’il faut se poser la question de la position de la première ligne, c’est tout simplement parce qu’une ligne de texte n’est pas un segment mathématique sans épaisseur : cette ligne a une hauteur.

Positionner la première ligne

Dans les illustrations suivantes, le trait rouge représentera la limite supérieure du rectangle d’empagement ; le trait bleu, la ligne de pied de la première ligne de texte.

Plusieurs solutions se présentent. Commençons par écarter les mauvaises.

Mauvaises solutions

Pour nous épargner tout calcul, la solution de facilité consisterait à utiliser l’interlignage comme distance entre le bord supérieur du rectangle d’empagement et la première ligne de pied. On voit immédiatement qu’il s’agit d’une très mauvaise idée : cette valeur est beaucoup trop importante ; le rectangle d’empagement concret (celui que voit le lecteur) se trouve significativement amputé. L’interlignage est destiné à séparer des lignes, non le bord supérieur du rectangle d’empagement de la première ligne.

Pour faciliter les calculs, une autre solution simple serait d’utiliser la force de corps de la police de labeur. Le résultat est assurément moins désastreux, mais il est loin d’être idéal, puisqu’il raccourcit encore un peu trop le rectangle d’empagement. Quelle serait dès lors une solution correcte ?

Un moindre mal

Il faut ici connaître les caractéristiques du logiciel utilisé. Ce dernier permet-il ou non au texte de dépasser du cadre qui l’accueille ?

Si ce n’est pas le cas, quelle serait la distance minimale qui permettrait d’afficher correctement la première ligne de texte, toujours à la même distance du bord supérieur ? Tout bonnement la hauteur, au-dessus de la ligne de pied, du glyphe le plus haut susceptible d’apparaître dans notre texte. Pour un texte français, il s’agira d’une capitale accentuée, généralement À ou Â.

Les À ou  n’étant pas d’une fréquence très élevée, on déplorera généralement une légère amputation verticale du rectangle d’empagement visible, mais dans des proportions qu’on est en droit de juger acceptables.

Bonnes solutions

L’idéal serait toutefois de pouvoir faire dépasser verticalement du cadre au moins les diacritiques des grandes capitales. Supposons que le logiciel utilisé le permette : n’y aurait-il pas de meilleures solutions encore ? Au moins deux.

Abstraction faite des capitales accentuées, quels sont les glyphes les plus hauts susceptibles d’apparaître dans un texte en français ? Contrairement à ce que l’on pourrait penser spontanément, il ne s’agit pas toujours des grandes capitales non accentuées, mais bien plus souvent des lettres avec ascendantes, comme b, d, h, l. Il faut toutefois s’en assurer pour la police de labeur utilisée. Si donc on choisit la hauteur des ascendantes, les seuls éléments susceptibles d’apparaître au-dessus du bord supérieur théorique du rectangle d’empagement sont les accents des grandes capitales, ce qui se produira relativement rarement et ne perturbera pas la perception qu’aura le lecteur des dimensions de la colonne de texte.

Une autre possibilité, visuellement très proche, serait d’opter pour la hauteur des grandes capitales non accentuées. On aura alors un débord vertical total des diacritiques, mais aussi un léger débord des ascendantes ou des parenthèses, sans que cela soit choquant pour l’œil. Si les deux options précédentes sont presque équivalentes, j’avoue avoir une préférence pour la seconde.

Reste une dernière possibilité : utiliser la hauteur d’x. En effet, les bas de casse (« minuscules ») sont de loin les lettres les plus fréquentes du texte courant. Si la justification n’est pas trop longue, que les phrases ne sont pas trop courtes, on peut même voir se succéder plusieurs lignes sans la moindre capitale. Les bas de casse déterminent donc en grande partie notre perception de la hauteur des lignes, surtout dans le cas des polices à grande hauteur d’x, où la différence de hauteur entre capitales et bas de casse est plus faible. Mais les lettres avec ascendantes ? Elles sont assez peu nombreuses, et la hauteur relative des ascendantes sera généralement d’autant plus faible que la hauteur d’x sera importante. Pour toutes ces raisons, on pourrait donc très bien préférer aux deux solutions précédentes le recours à la hauteur d’x — c’est mon cas.

Contourner une limitation technique

Les trois solutions précédentes sont-elles pour autant inaccessibles aux logiciels qui ne permettraient pas de faire dépasser du texte des cadres ? Pas du tout, car il n’est pas difficile de contourner cette limitation.

La solution consiste à appliquer une correction au blanc de tête qui augmentera la hauteur du rectangle d’empagement théorique : il s’agit, autrement dit, de réduire la marge supérieure.

Pour déterminer cette correction, il faut, dans l’ordre :

• opter pour l’une des trois bonnes solutions présentées ;
• utiliser comme distance la hauteur du plus grand glyphe susceptible d’apparaître dans un texte en français (À ou Â, généralement, selon la police) ;
• calculer la correction en soustrayant de cette hauteur celle que l’on aurait adoptée avec un logiciel permettant le dépassement.

Soit T le blanc de tête initial, T′ le blanc de tête corrigé, C, la correction à appliquer, hgmax, la hauteur au-dessus de la ligne de pied du plus grand glyphe susceptible d’apparaître dans le texte, et ds la distance que l’on aurait souhaitée entre le bord supérieur du rectangle d’empagement et la première ligne de pied :

C = hgmax − ds

T′ = T − C = T − (hgmax − ds) = T − hgmax + ds

Attention, par la suite, il conviendra de prendre en compte la nouvelle hauteur du rectangle d’empagement théorique, Ht′, soit Ht′ = Ht + C = Ht + hgmax − ds.

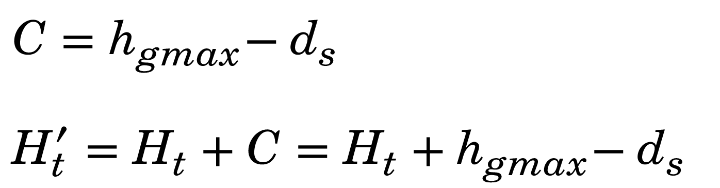
Quelle position pour la dernière ligne ?

En l’absence de correction de l’interlignage, la dernière ligne n’atteindra pas le bord inférieur du rectangle d’empagement théorique, amputant le rectangle d’empagement visible d’une hauteur variable pouvant approcher un interlignage. Pour que la hauteur de la colonne de texte coïncide avec celle du rectangle d’empagement théorique, on a bien compris qu’il fallait ajuster cet interlignage, afin de caler la dernière ligne sur le bord inférieur.

Seulement, de quelle manière ?

On peut imaginer deux possibilités : soit positionner la dernière ligne pour que ses descendantes reposent sur le bord inférieur du rectangle d’empagement, soit faire en sorte que ce bord se confonde avec la ligne de pied.

Parce que les descendantes sont rares (g, j, p, q, y), on peut estimer que la ligne de pied joue un rôle bien plus important pour la perception de la hauteur des lignes, et donc que la deuxième solution est nettement préférable à la première.

Calculer le nombre de lignes du rectangle d’empagement

Une fois déterminée la position de la première ligne et de la dernière ligne, on peut calculer le nombre de lignes que présentera notre colonne de texte. Soit n ce nombre de lignes, Ht la hauteur du rectangle d’empagement théorique (éventuellement corrigée comme vu plus haut), ds la distance séparant le bord supérieur de la première ligne de pied, di la distance séparant la dernière ligne de pied du bord inférieur (soit 0, soit la hauteur de la plus grande descendante) et i2 l’interlignage provisoire calculé dans le billet précédent.

Pour calculer le nombre entier n, il faut avoir en tête qu’il est égal au nombre d’interlignages plus un : un interlignage suppose deux lignes ; deux interlignages, trois lignes, etc. On calcule le nombre d’interlignages (n − 1) en divisant par i2 la hauteur disponible pour ces (n − 1) lignes, soit (Ht − ds − di), qui est la distance entre la première ligne de pied et la dernière. La hauteur de ces (n − 1) lignes doit être inférieure ou égale à (Ht − ds − di). Comme (n − 1) doit être un nombre entier, on arrondira donc le quotient obtenu à l’entier naturel inférieur, ce qui revient à prendre sa partie entière. Voilà qui en mathématiques se note ⌊x⌋.

Donc : n = ⌊(Ht − ds − di) ÷ i2⌋ + 1

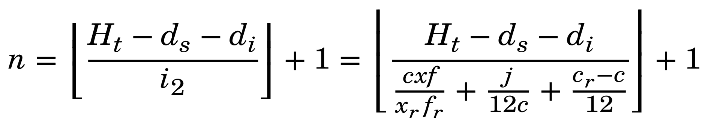
Ajuster l’interlignage

Pour finir, il ne reste plus qu’à calculer l’interlignage afin qu’il corresponde à ce nombre entier de lignes. On soustrait 1 à n dans la mesure où la première ligne n’est pas positionnée en fonction de l’interlignage.

i = (Ht − ds − di) ÷ (n − 1)

La formule complète est donc :

i = (Ht − ds − di) ÷ ⌊(Ht − ds − di) ÷ ((c · x · f) ÷ (xr · fr) + j ÷ 12c + (cr − c) ÷ 12)⌋

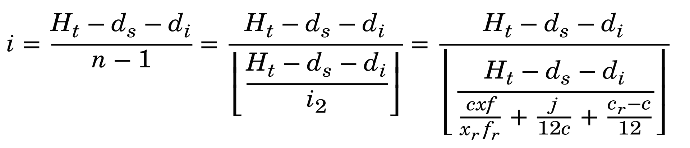
Formule provisoire, toutefois, je le rappelle, car il devrait être possible de faire mieux pour le calcul de i2, en intégrant la graisse et l’angle des axes de la police de labeur. Cependant, même alors, ce sera toujours au metteur en page de trancher : il ne faudrait pas voir dans ces calculs laborieux un carcan, mais au contraire une aide, un moyen de gagner du temps.

Du temps ? Peut-être êtes-vous fâché avec les mathématiques ? Vous pensez que tout cela représente bien trop de peine pour pas grand-chose ? C’est sans doute oublier que l’informatique permet ensuite de ne plus y revenir.

Il suffit en effet d’utiliser un tableur pour entrer ces formules dans une feuille de calcul, ou bien d’écrire un script dans le langage informatique de son choix, et le tour est joué. Aussi, oui, l’effort investi finit par faire gagner beaucoup de temps : à un auteur autoédité, sans doute pas, mais à un éditeur ou à un metteur en page certainement.

Vous ne savez pas programmer ? Demandez à une IA : pour une tâche aussi simple, le programme généré devrait être correct — par exemple, en Python ou en Lua.

Vous ne savez pas utiliser les tableurs ? Pour des calculs de cette nature, cela n’a rien de difficile. Vous pouvez par exemple faire appel à Calc de LibreOffice, suite bureautique libre et gratuite. Des tutoriels en ligne vous aideront à le prendre en main.

Vous pouvez également nous contacter si vous souhaitez recevoir une feuille de calcul clés en main.

Avec ce billet s’achève la série consacrée à l’interlignage. Nous aborderons la prochaine fois un sujet bien plus simple : les en-têtes et pieds de page.