Réussir une mise en page. — L’interlignage (3)

Dans les deux billets précédents, nous avons vu l’importance, pour la lisibilité, de la distance entre deux lignes consécutives (l’interlignage), et qu’on ne pouvait pas se fier à la valeur par défaut proposée par la plupart des logiciels. Le logiciel ConTeXt obtient un bien meilleur résultat en s’appuyant sur la hauteur d’x, mais néglige d’autres paramètres significatifs. De son côté, James Felici propose une méthode pour faire dépendre l’interlignage de la longueur des lignes, qui toutefois n’intègre pas la hauteur d’x et néglige le principe, qu’il connaît pourtant bien, que « l’espace séparant les lignes […] semble augmenter plus vite que le texte » (autrement dit, que l’interlignage d’un texte composé dans un petit corps doit être proportionnellement plus important que celui d’un texte composé dans un plus grand corps).

Ce billet proposera d’améliorer la formule de Felici en intégrant à la fois hauteur d’x et variation proportionnelle au corps de la police utilisée.

Démarche

Pour écrire cette formule, nous avons besoin d’une fonte de référence, dans un corps donné. Dans la mesure où les garaldes ont fait leur retour en force dans l’édition littéraire, j’ai opté pour l’EB Garamond 12 pt de Georg Duffner, à ma connaissance le plus beau Garamond libre disponible. Sa hauteur d’x est de 405 millièmes de cadratin, soit 0,405 em. Pour tenir compte de cette hauteur d’x, nous allons prendre par ailleurs comme référence le facteur choisi par Hans Hagen pour ConTeXt : 2,8 — sachant que la plupart du temps, pour le français, c’est un facteur supérieur qui sera utilisé.

Calcul

Soit i2 l’interlignage provisoire à calculer, c la force de corps de la police utilisée, et j la justification, toutes ces mesures étant exprimées en points. On commence par reprendre le début de la formule de Felici : i2 = c + (j ÷ 12c). Au lieu toutefois de simplement partir de la force de corps, nous allons appliquer à celle-ci un premier facteur considérant la hauteur d’x, calculé comme suit. Soit x la hauteur d’x exprimé en cadratins de la police utilisée et xr la hauteur d’x de la police de référence, également en cadratins : on multiplie c par le rapport x∕xr. Si x > xr, l’interlignage sera plus grand, plus petit dans le cas contraire.

On multiplie ensuite le résultat par un autre rapport, celui du facteur d’interlignage utilisé sur le facteur d’interlignage de référence (Hans Hagen : 2,8). Soit f le facteur appliqué à la hauteur d’x de la police choisie et fr le facteur de référence : ce deuxième rapport par lequel on multiplie c est donc f∕fr . L’interlignage se trouvera augmenté si f > fr, diminué dans le cas contraire. On ajoute à présent le deuxième terme de la formule de Felici, intégrant la justification : j ÷ 12c.

Reste à prendre compte la force de corps utilisée (c), en commençant par soustraire la force de corps de la fonte utilisée à celle de référence (cr) : cr − c. Sauf résultat nul (quand c = cr), la valeur obtenue est bien trop grande pour être ajoutée à l’interlignage provisoire obtenu par les calculs précédents. Il convient de pondérer ce paramètre en le divisant par un nombre positif. À la suite d’essais empiriques, j’ai constaté que 12 donnait des résultats satisfaisants pour la plupart des polices testées : (cr − c)∕12​.

Ainsi proposé-je la formule suivante : ​i2 = (c × (x ÷ xr) × (f ÷ fr)) + (j ÷ 12c) + (cr − c) ÷ 12. Soit i2 = (c · x · f) ÷ (xr · fr) + (j ÷ 12c) + (cr − c) ÷ 12.

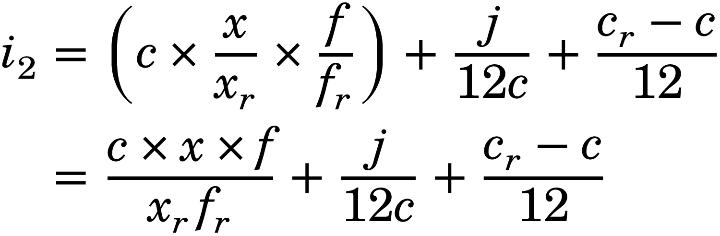
Exemple d’utilisation pour une composition en Noto Serif 11 pt (hauteur d’x de 0,536 em) et une justification de 100 mm (1 mm ≃ 2,834 67 pt DTP) :

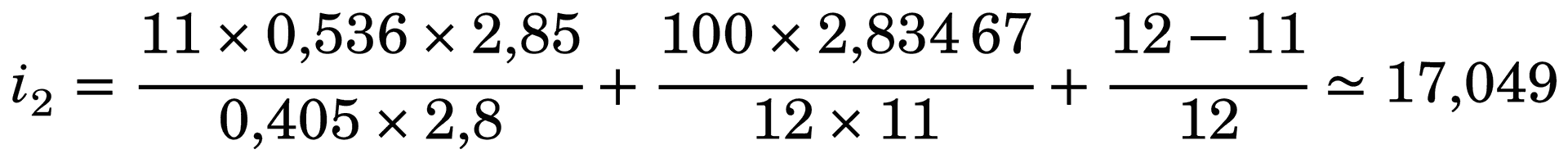
Exemple de calcul de l’interlignage avec la formule « Felici-Savary » provisoire.

Application pratique du calcul précédent.

Limites

Cette formule « Felici-Savary » fonctionnera-t-elle toujours parfaitement ? Hélas, non. Certes, elle donnera un interlignage satisfaisant dans un bien plus grand nombre de cas que l’interlignage automatique de 120 %. Hélas, elle ne prend pas en compte d’autres paramètres susceptibles d’influencer l’interlignage :

• la chasse moyenne (largeur moyenne des glyphes) ;
• la graisse (épaisseur moyenne des traits des glyphes) ;
• la hauteur des grandes capitales.

Chasse

Prendre en compte la chasse n’est pas très difficile ; à l’usage, toutefois, j’ai constaté que cela ne servait à rien pour les polices de labeur que j’ai testées.

On peut en effet considérer qu’en pratique la hauteur d’x prend déjà en compte la chasse : de fait, lorsque des glyphes chassent beaucoup, c’est en général parce qu’ils présentent également une hauteur d’x élevée. Si tel n’était pas le cas, cela impliquerait des glyphes aux proportions inhabituelles. Or, les polices de labeur, parce qu’elles sont tenues à une certaine discrétion et sobriété, présentent un grand nombre de caractéristiques communes, à commencer par les proportions des caractères. Et même si certaines proposent des glyphes un peu plus étroits ou plus larges que la moyenne pour une hauteur d’x équivalente, cette variation demeure modeste.

Dans la mesure où la hauteur d’x apparaît bien plus déterminante pour le calcul de l’interlignage, l’ajustement en fonction de la chasse se révèle comparativement infime pour la plupart des polices de labeur. Au reste, l’étape finale consistant à ajuster l’interlignage en fonction du nombre de lignes que peut accueillir le rectangle d’empagement annulera très souvent la petite variation associée.

J’ai dès lors estimé inutile d’alourdir inutilement la formule qui précède.

Graisse

La graisse devrait quant à elle impacter davantage l’interlignage. Plus une police est grasse, plus l’interlignage devra être important. Hélas, les métriques des fontes ne contiennent pas cette information, qui ne saurait donc être extraite directement des fichiers, à la différence de la hauteur d’x ou de la position de la ligne de pied.

Comment dès lors mesurer la graisse pour la mettre en équation ? Il faudrait écrire un programme pour analyser une sélection de glyphes représentatifs afin d’estimer cette graisse, puis pondérer ce nouveau facteur de manière empirique jusqu’à obtenir des résultats satisfaisants. J’ai prévu de m’y employer, avec l’aide de personnes plus compétentes que moi en informatique.

Hauteur des grandes capitales

S’agissant de la hauteur des grandes capitales, nous avons déjà pris en compte les plus hautes, les capitales accentuées du français (généralement celles avec un accent grave ou circonflexe), pour augmenter au jugé le facteur f. Il est vrai qu’il serait plus satisfaisant d’intégrer à la formule la hauteur maximale des capitales utilisées en français pour ne pas avoir à se préoccuper de la valeur de f. Cela suppose d’extraire de la fonte la hauteur de la plus grande capitale accentuée utile en français — d’autant que cette information est utile pour la dernière étape.

Reste cela dit un dernier paramètre à intégrer dans le calcul de l’interlignage…

Verticalité

La verticalité de certaines polices demande un interlignage en accord avec celle-ci : plus important, donc. Mais de quoi s’agit-il ?

On s’en doute, les caractères de Gutenberg et des imprimeurs de la Renaissance n’ont pas surgi de nulle part : le modèle du livre imprimé n’était autre évidemment que le manuscrit médiéval. Ainsi la calligraphie a-t-elle en grande partie déterminé le dessin des premiers caractères. On écrivait alors à la plume : en fonction de l’angle de cette dernière, de la pression exercée et de la vitesse du tracé, la pointe biseautée produisait des pleins et des déliés, respectivement les parties épaisses et les parties fines du trait.

Pleins (noir) et déliés (rouge) du a du Trianon Text de Loïc Sander.​​

C’est la répartition des pleins et des déliés qui détermine l’axe d’un caractère donné. Les premières polices de caractères présentaient des axes nettement inclinés à gauche. Au fil du temps, à mesure que la typographie s’émancipait du modèle calligraphique, ces axes se sont redressés pour devenir verticaux, et même disparaître dans les polices d’écriture au trait constant, sans pleins ni déliés.

Évolution de l’axe du o au fil des polices d’écriture.

Est-il possible d’automatiser l’ajustement de l’interlignage en fonction de l’angle des axes de la police utilisée ? Cette information ne figure malheureusement pas plus que la graisse dans les métriques des fontes et ne saurait donc être extraite directement des fichiers. Pour déterminer cet ajustement, il faudrait donc là encore un programme en mesure d’analyser les glyphes (représentation graphique des caractères en typographie numérique) et de calculer cet angle moyen afin d’y appliquer un facteur qui resterait à préciser (sur la base d’essais concrets en vue de trouver un interlignage idéal — comme l’a fait Hans Hagen avec son facteur de 2,8 pour ConTeXt). Voilà qui n’a rien d’impossible. À terme, la formule proposée sera donc améliorée pour convenir à un plus grand nombre de cas encore.

Pour l’heure, quand l’interlignage obtenu ne convient pas, je me contente de jouer avec la valeur de f : au lieu de 2,8 ou de 2,9, j’applique par exemple au jugé un facteur de 3, voire un peu plus pour un texte composé dans une didone comme le Trianon de Loïc Sander (police aux axes quasiment verticaux).

Dans l’exemple suivant, la première colonne est composée en Trianon Text avec l’interlignage que donne la formule « Felici-Savary » pour un facteur f de 2,85 (15,54 pt). Le résultat est un pavé légèrement étouffant. La deuxième colonne est composée avec un interlignage de 16,5 pt : le texte respire.

Exemple d’échec de la formule « Felici-Savary » (à gauche).

Retenir

Il n’existe pas de solution magique pour calculer l’interlignage. Si la formule « Felici-Savary » que je propose conviendra dans un bien plus grand nombre de cas que l’interlignage automatique d’InDesign, de LaTeX et de ConTeXt ou même que la formule Felici de base, nous avons vu qu’elle ne prenait pas tout en compte. Il faut voir l’interlignage obtenu comme un simple point de départ, une proposition. In fine, c’est l’œil qui jugera si telle ou telle valeur convient ou non.

Dans le prochain et dernier billet sur l’interlignage, nous expliquerons enfin comment ajuster ce dernier pour que le nombre de lignes d’une page pleine corresponde exactement à la hauteur du rectangle d’empagement.