Réussir une mise en page. — L’interlignage (2)

Le billet précédent soulignait l’importance de l’interlignage pour la lisibilité du texte courant, à savoir la distance entre deux lignes de pied consécutives, avant de pointer deux problèmes que posent les interlignages par défaut de la plupart des logiciels : non seulement cette valeur ne convient pas à toutes les polices, mais elle ne permet pas au texte courant d’occuper toute la hauteur disponible du rectangle d’empagement, donnant ainsi naissance à des rectangles tronqués, ce qui gâche en partie l’empagement défini.

Avant d’ajuster l’interlignage à la hauteur du rectangle d’empagement pour que celle-ci corresponde à un nombre entier de lignes, encore convient-il de partir d’une valeur adéquate.

Au temps de la typographie au plomb, l’interlignage était égal au minimum à la force de corps. On augmentait cette valeur en ajoutant des interlignes (nom féminin), à savoir des lames métalliques placées entre deux lignes consécutives. La typographie permet des interlignages inférieurs à la force de corps, mais ce ne serait pas pertinent pour la composition du texte courant. Nous considérerons donc que l’interlignage devra être nécessairement supérieur ou égal à la force de corps de la police utilisée.

Pour fixer un interlignage adapté, nous avons vu qu’il fallait pour commencer se fonder sur la hauteur d’x de la police utilisée. Soit i1 l’interlignage initial, c, la force de corps utilisée (en points), x la hauteur d’x en cadratins et f le facteur utilisé : i1 = (xc) × f.

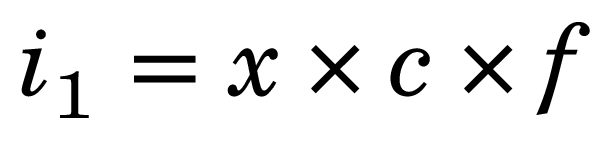
Par exemple, pour une fonte de corps 12 dont la hauteur d’x serait de 405 millièmes de cadratin, soit 0,405 em, l’interlignage i1 serait :

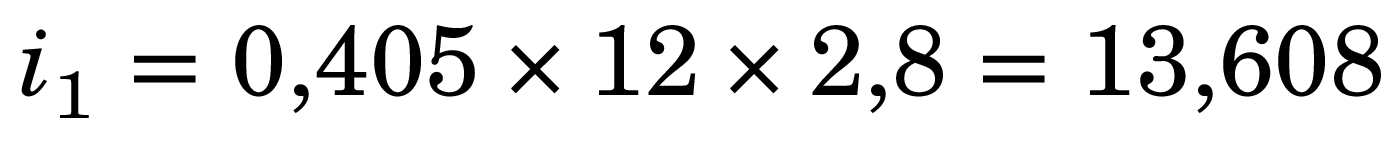
On a vu que pour le français, qui comporte des grandes capitales accentuées comme  ou Ê, il convenait généralement d’appliquer plutôt un facteur compris entre 2,85 et 3 selon la hauteur des accents de la police choisie et la longueur des descendantes de lettres comme p, q, y : il s’agit en effet d’éviter la collision ou du moins une trop grande proximité entre les diacritiques et ces descendantes. Ce facteur, qui dépendra de la police choisie, devra être déterminé sur la base d’essais et erreurs. Les polices aux descendantes courtes ou aux accents à faible pente pourraient s’accommoder du facteur de 2,8 (voire un peu moins), tandis que d’autres nécessiteront un facteur supérieur.

Si l’on reprend l’exemple précédent avec un facteur de 2,9, alors i1 serait cette fois :

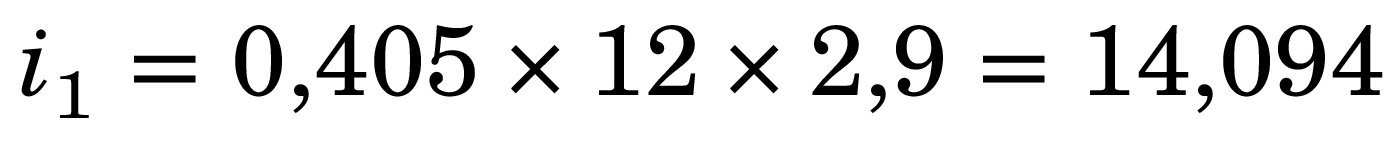
Plutôt qu’une valeur dépendant uniquement de la force de corps, on obtient avec cette formule un interlignage adapté à la police utilisée, qui conviendra esthétiquement dans un bien plus grand nombre de cas que l’interlignage automatique de la plupart des logiciels.

Si toutefois nous utilisons une police à la faible hauteur d’x comme le Guillaume, il est très possible que l’interlignage ainsi calculé soit inférieur à la force de corps. Dans ce cas, on prendra la force de corps comme interlignage initial : i1 = c.

Notons au passage que l’interlignage définitif que nous allons calculer ne devra pas être inférieur à cet interlignage initial i1, en raison des capitales accentuées du français.

Mais la seule prise en compte de la hauteur d’x ne suffit pas…

Justification

En effet, l’interlignage devrait dépendre également de la justification. Deux exemples pour en prendre conscience :

Composition étroite en EB Garamond 12 pt. — L’interlignage de 14,4 pt paraît un peu trop grand.

Composition large en EB Garamond 12 pt. — L’interlignage de 14,4 pt est un peu trop faible.

Rappelons que plus une ligne est longue, plus le risque est important de rater la ligne suivante. C’est la raison pour laquelle il convient d’augmenter l’interlignage pour faciliter au lecteur arrivé en fin de ligne le repérage de la ligne suivante.

En appliquant les recommandations du typographe James Felici pour prendre en compte la longueur des lignes, on pourrait calculer l’interlignage i2 de la façon suivante : i2 = c + (j ÷ 12c) — avec c la force de corps de la police utilisée, exprimée en points, et j la justification, également en points (sachant que 1 mm ≈ 2,834 67 pt DTP ≈ 2,845 26 pt TeX).

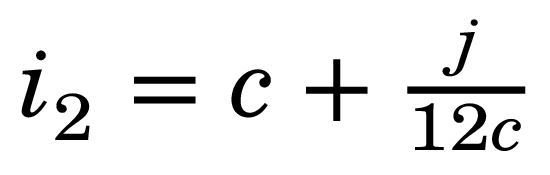
Felici recommande d’arrondir au demi-point le plus proche. À l’ère toutefois de la typographie numérique, où les mesures peuvent être calculées avec précision et stockées dans des variables pour ensuite être appelées sans avoir à saisir le moindre nombre, j’estime ce conseil non seulement inutile mais contre-productif — surtout à la dernière étape, où il s’agira d’ajuster l’interlignage à la hauteur du rectangle d’empagement pour faire correspondre exactement celle-ci à un nombre entier de lignes. L’informatique permet une précision qui aurait fait rêver les imprimeurs d’autrefois : pourquoi refuser d’en tirer parti ?

Prenons pour exemple une justification de 100 mm et une fonte de 12 pt DTP :

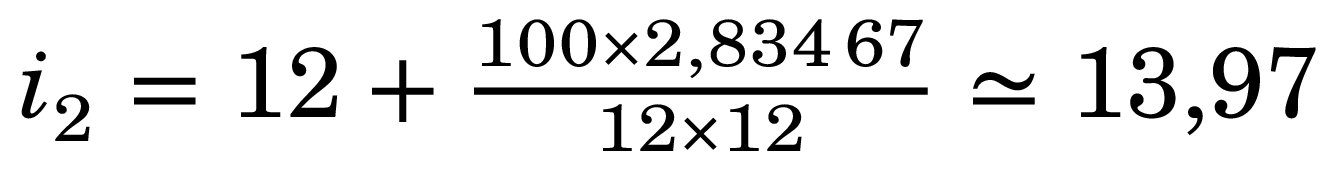
On voit que le résultat est presque identique à celui qu’on obtenait plus haut en suivant la méthode de Hans Hagen, avec un facteur de 2,9. Mais cette proximité est trompeuse…

Certes, la formule dérivée du Manuel complet de typographie de Felici constitue un net progrès par rapport aux interlignages automatiques généralement proposés, mais le lecteur vigilant aura noté que, hélas, le calcul proposé omet d’intégrer la hauteur d’x, ce qui est d’autant plus regrettable que le manuel de Felici ne manque pas de préciser par ailleurs l’importance de celle-ci pour l’interlignage.

La formule du typographe américain donnera ainsi le même résultat que l’on utilise le Guillaume ou le Noto Serif… Elle ne conviendra donc que pour des polices moyennes, donnant de mauvais résultats pour les polices aux hauteurs d’x très différentes.

C’est la raison pour laquelle on pourrait améliorer cette formule en intégrant ce paramètre. Mais attendons… car justification et hauteur d’x ne sont pas les seuls points à considérer.

Corps

Pour citer encore James Felici, « l’espace blanc, y compris l’espace séparant les lignes, semble augmenter plus vite que le texte ». Autrement dit, pour ce qui nous intéresse ici, plus la force de corps augmente, plus l’interlignage devrait diminuer, et inversement. Reste à estimer dans quelle proportion.

Dans le prochain billet, nous verrons ainsi comment améliorer la formule de Felici en intégrant à la fois la hauteur d’x et la force de corps de la police utilisée.