Réussir une mise en page. — L’empagement (2)

Mis à jour le 16-1-2025 à la suite d’informations apportées par G. Barot.

Dans les billets précédents, je soulignais l’importance du format et l’existence d’un lien entre celui-ci et l’empagement (consistant à décider de la taille des marges pour définir les dimensions du rectangle d’empagement et sa position sur la page). L’empagement découle en effet essentiellement du format, et certains formats se prêtent mieux à certains empagements que d’autres, comme l’usage permet de s’en rendre compte.

Quelle que soit la méthode retenue, le texte n’est pas centré sur la page, mais normalement plus près du haut que du bas de la page, et plus près de la reliure que de l’extérieur — sachant qu’en fonction du procédé de reliure adopté, une correction des marges interne et externe pourrait s’avérer nécessaire, ce qui fera l’objet d’un futur billet.

 On peut classer les méthodes d’empagement en deux grandes catégories : les constructions géométriques et les méthodes arithmétiques.

Constructions géométriques

Au Moyen Âge, les empagements étaient obtenus par construction géométrique ne requérant aucune mesure : les tracés régulateurs. La méthode aujourd’hui la plus connue est celle du canon de division harmonieuse, traditionnellement attribuée, au moins depuis le typographe Jan Tschichold, à l’architecte du treizième siècle Villard de Honnecourt.

Gilles Barot rapporte toutefois qu’en réalité on doit à l’architecte allemand Hans Hammer les premiers tracés explicites conservés, qui datent de la fin du quinzième siècle, dans le carnet (Musterbuch) de celui qui fut maître d’œuvre de la cathédrale de Strasbourg. Historien de l’art et conservateur du Kunstmuseum de Bâle, Walter Ueberwasser aurait été le premier au vingtième siècle à comprendre et à utiliser ce canon (Von Mass und Macht der alten Kunst, 1933). « La fécondité de ce tracé, conclut Gilles Barot, est en voie de reconnaissance par la communauté scientifique, comme le montrent les travaux de l’équipe universitaire de Liverpool (R.-U.) sur la géométrie des voûtes. »

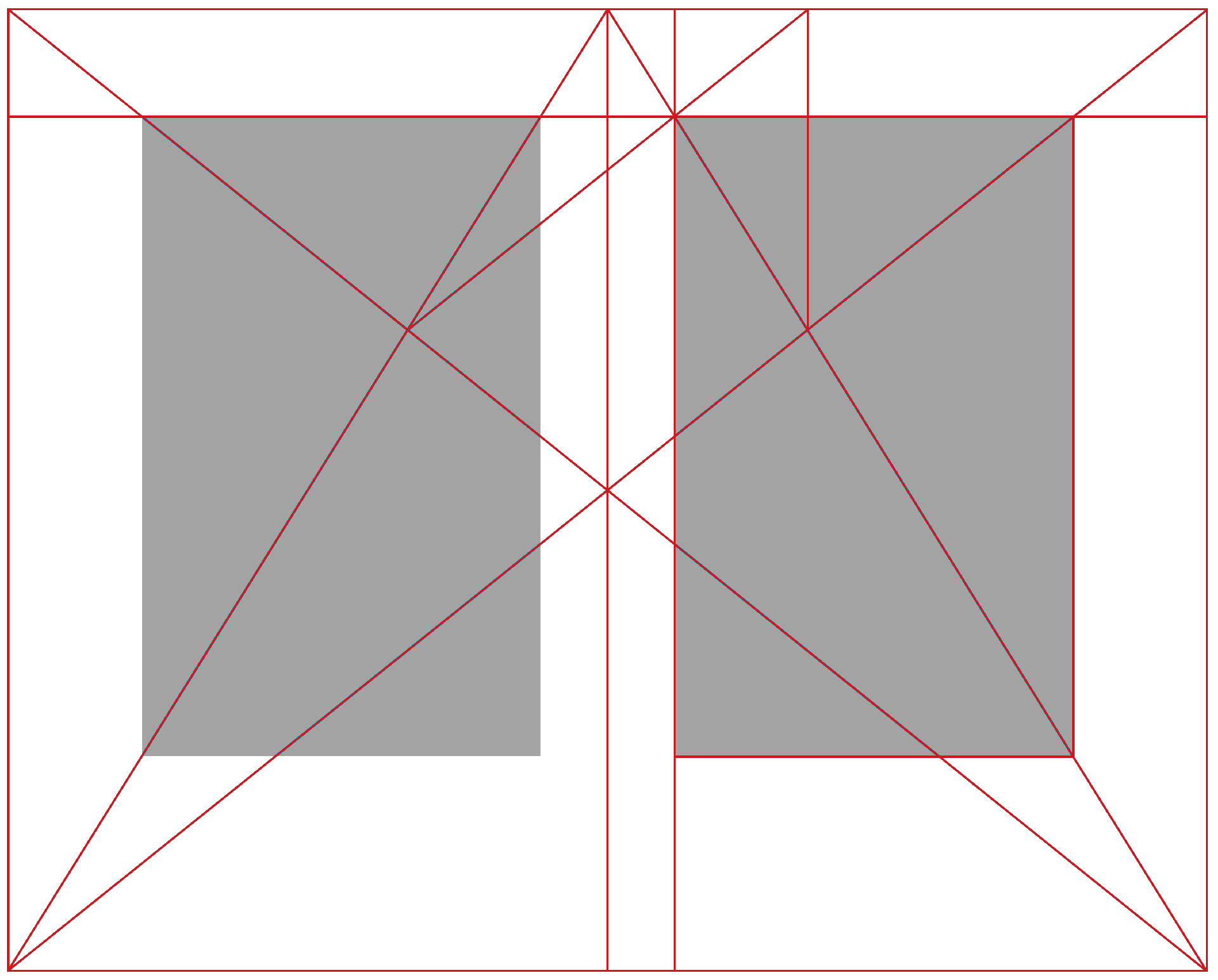
Canon de division harmonieuse. — Tracés régulateurs.

On peut observer que le rectangle d’empagement présente les mêmes proportions que celles de la page. Il est par ailleurs positionné de sorte que le petit fond est égal à la moitié du grand fond et le blanc de tête à la moitié du blanc de pied.

Les rectangles matérialisés en jaune ci-dessous sont bien entendus invisibles, et pourtant enregistrés à notre insu par notre cerveau : les rectangles supérieurs a, b et c présentent les mêmes proportions que celles de la double page ; les rectangles inférieurs A, B et C, les mêmes proportions que celles de la page.

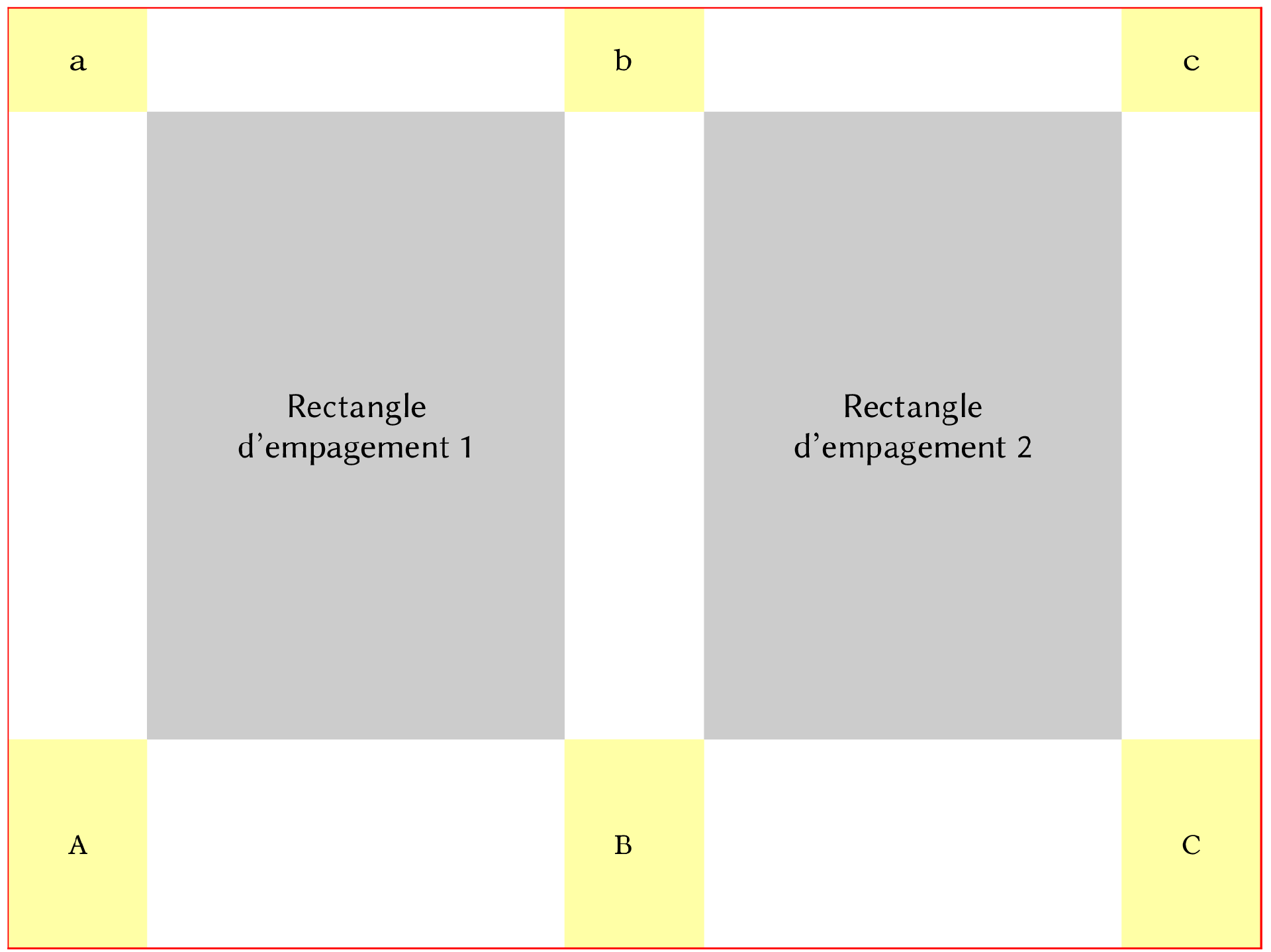
Canon de division harmonieuse. — Rectangles en harmonie.

On voit que cette méthode d’empagement n’a pas usurpé son nom.

Après des siècles d’oubli, ces techniques ont pu être redécouvertes au vingtième siècle par Walter Ueberwasser, et l’empagement correspondant être reproduit de différentes manières par des typographes comme Johannes Alexander van de Graaf, Raúl Rosarivo et Jan Tschichold.

Tschichold considère cet empagement comme particulièrement adapté aux formats 2:3 et 3:4 (rapport hauteur sur largeur de 1,5 ou de 1,33). C’est alors en effet que non seulement la page, mais aussi la double page (et les rectangles a, b et c) présentent ce que Tschichold appelle des « proportions claires », respectivement 4:3 et 3:2 . Par ailleurs, dans un format 2:3, la hauteur du rectangle d’empagement est égale à la largeur de la page ; dans un format 3:4, c’est la largeur du rectangle d’empagement qui est égale, quant à elle, à la moitié de la hauteur de la page.

Les autres caractéristiques du canon de division harmonieuse que nous présentions se retrouvent cependant dans tous les formats.

Il existe cela dit des empagements très différents, basés sur d’autres tracés régulateurs. On pourrait citer ceux, complexes, de Jay Hambidge, présentés dans le livre Maquette et Mise en page de Pierre Duplan et Roger Jauneau (édition de 1982).

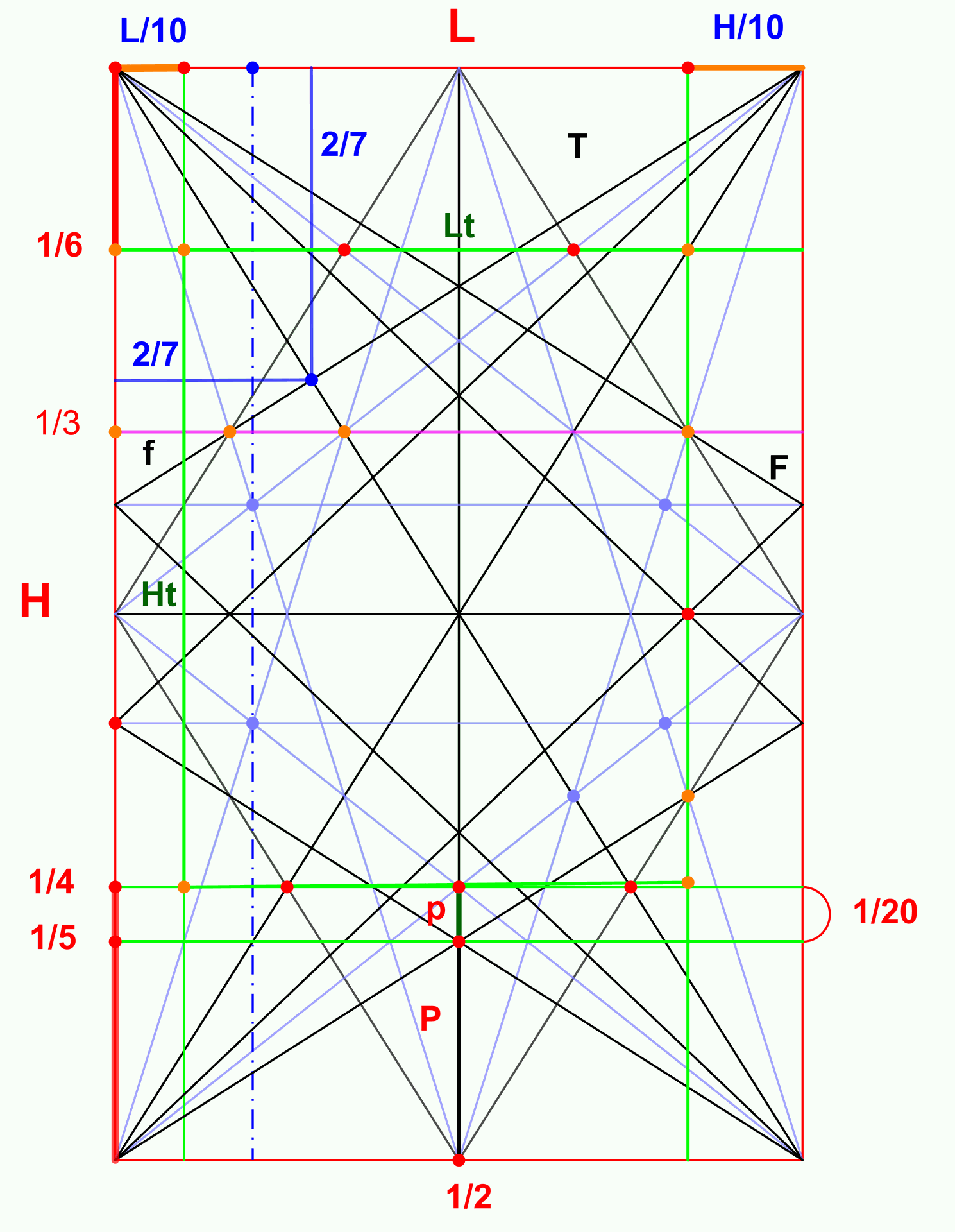
Restitution de l’empagement de Hambidge par G. Barot, 2024, d’après Duplan et Jauneau, 1982.

Mais je propose que nous nous attardions plutôt sur l’empagement original, plus récent, déterminé par un hexagone régulier ayant pour base la largeur de la page, du typographe Robert Bringhurst dans son classique Principes élémentaires de la typographie.

En 2024, Gilles Barot, webmestre du site Géométrie sensible (https://www.geometriesensible.com/), en a produit une analyse détaillée, permettant de recréer par de simples calculs cet empagement basé sur la racine carrée de 3. À l’ère de la dématérialisation et de la typographie numérique, on recourt en effet plus volontiers aux méthodes arithmétiques (liées ou non à de tels tracés régulateurs, qui peuvent in fine se voir réduire à une série de calculs).

Nous y reviendrons dans le prochain billet.

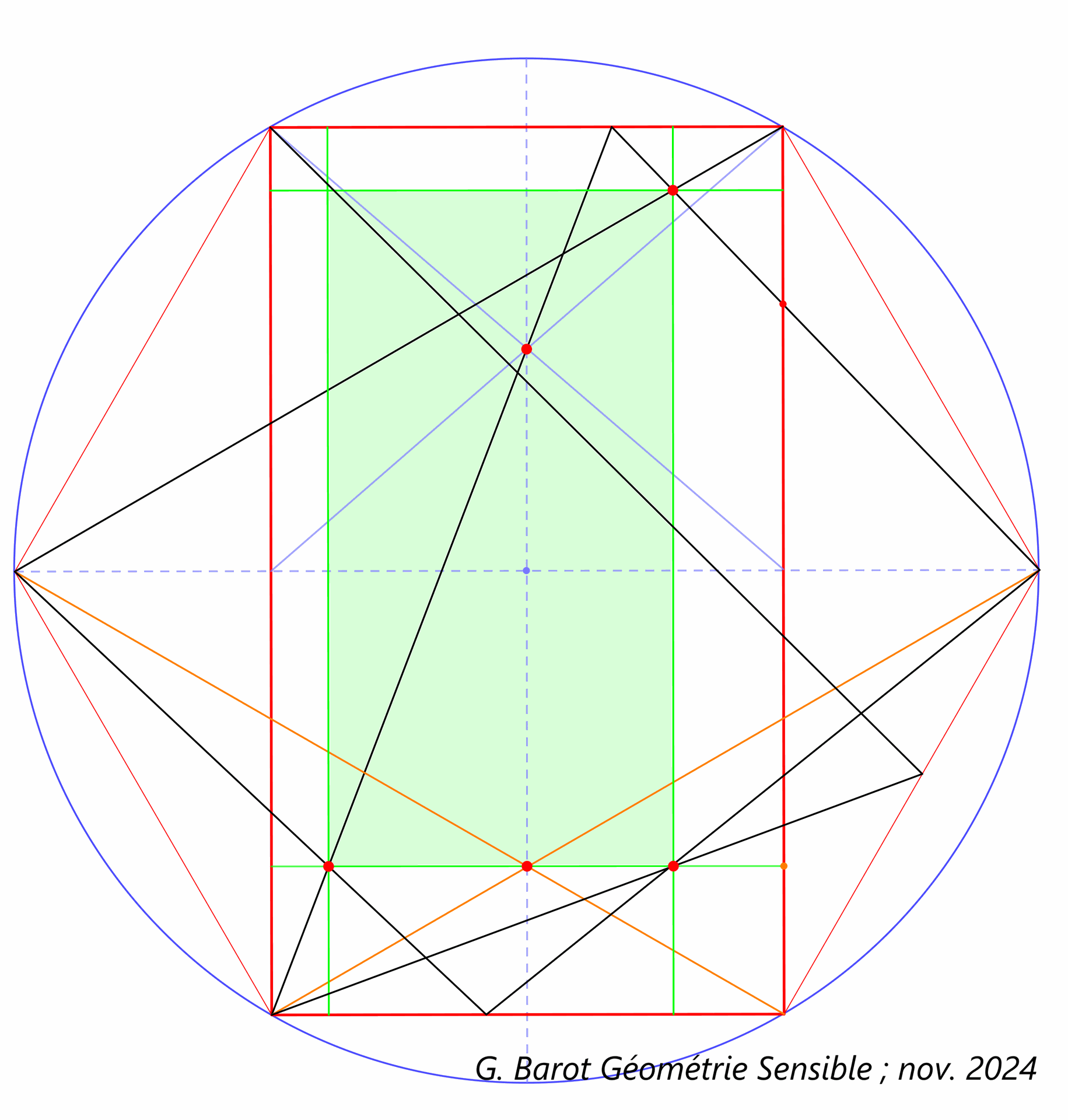
Restitution de l’empagement de Bringhurst par G. Barot, 2024, d’après le schéma de la maquette de Principes élémentaires de la typographie, p. 6.